小北
0%

Trie树

发表于 更新于 分类于

本来是想先完成平衡树的blog的，但是，我不会。。。就先完成Trie树的学习吧！

字典树基础介绍

  • 关于
    字典树又称单词查找树，Trie树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高。
  • 性质

1.根节点不包含字符，除根节点外每一个节点都只包含一个字符；
2.从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串；
3.每个节点的所有子节点包含的字符都不相同。

  • 应用
    应用在串的快速检索、“串”排序、最长公共前缀这些方面，作为其他数据结构的辅助结构（后缀树，AC自动机……）（接下来我要记录的是串的快速检索。后面的等我以后学习了再加入进来。）
    ——来自百度百科

引入

在给定的几个单词中去查找时候出现过某一个单词或者某些单词，当单词数量较少时，我们也依然可以暴力的去匹配和枚举，但当字符串多，按暴力的方法就不太可行了，所以来学习Trie树。

eg:给你6个单词abbe,abde，abc，abcd,hope，help. 然后再给你多个单词比如abbe，hel，abc，cook，问它是否在已给出的单词中出现过？

建树

首先创造一个根节点，然后根据单词abbe,abde，abc，abcd,hope，help一次去建立，建立过程如下：由第一个单词abbe，首先查询根节点下面是否有节点a，显然第一个没有，所以我们要建立节点a，然后在相应的往a节点后建立节点b，b,e;在把第一个单词建立完成之后，我们要对最后一个e做标记，代表他是一个单词的最后一个，后面再搜索是否有的时候，就会用到这个标记，对第二个单词abde,我们发现根节点下面有a,a的节点下面也有b,但b下面却没有d,所以我们在b节点下面建立节点d，依次类推，将后面的单词这样建立下来，就有了下面的这样一颗树。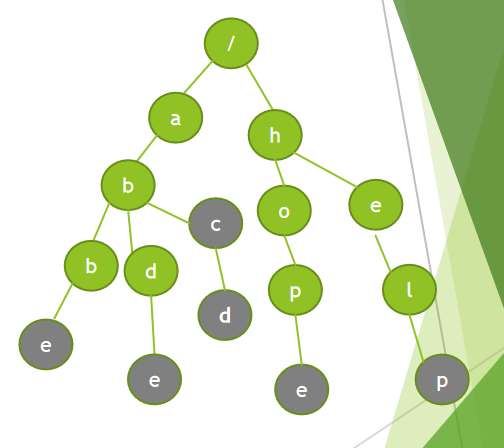
alt

代码如下:

定义节点结构体 

1
2
3
4
5
6
7
8
9
10
struct node{
	node* next[26];       //指向二十六个字符（a-z分别被0-25表示） 
	int cnt,i;
	node()
	{
		cnt=0;
		for(i=0;i<26;i++)
		next[i]=NULL;      //指针赋初值为NULL 
	} 
};

插入给出的字符串

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void insert(node* root,char s[]) 
{
	int ls=strlen(s);
	int i=0;
	node *p=root;
	for(i=0;i<ls;i++)
	{
		int c=s[i]-'a'; 
		if(p->next[c]==NULL)//如果不存在就创造一个 
		{
			p->next[c]=new node();
		}
		p=p->next[c];
	}
	p->cnt++;   //标记加一，代表字符串出现的次数 
}

查询

查询第一个单词，abbe,我们从上面的图来看，abbe出现在前面的字符串中，而对于hel，我们会发现hel按照我们的查询，每个字符都出现了，但实际上，原字符串中是没有hel的这个字符串，所以我们就了解上面为什么在建树的过程中我们将字符串的最后一个单词做标记，这就可以使我们正确查询是否出现过待查询单词。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int search(node* root,char s[])
{
	int i=0;
	int ls=strlen(s);
	while(i<ls)
	{
		int c=s[i]-'a';
		if(root->next[c]==NULL)//如果字符串中某个字符没有，则已经k可以认定没有出现 
			return 0;
		else
			root=root->next[c];
		i++;
	} 
	return root->cnt; 
}
  • 搜索字典树方法
    搜索字典项目的方法为：
    (1) 从根结点开始一次搜索；
    (2) 取得要查找关键词的第一个字母，并根据该字母选择对应的子树并转到该子树继续进行检索；
    (3) 在相应的子树上，取得要查找关键词的第二个字母,并进一步选择对应的子树进行检索。
    (4) 迭代过程……
    (5) 在某个结点处，关键词的所有字母已被取出，则读取附在该结点上的信息，即完成查找。
    ——来自百度百科

删除字符串

在字典树中删除字符串有三个情况，第一种是那个节点下面只有一个字符串，那么我们直接对节点进行删除即可，将整个字符串删除，第二种，一个字符串出现多次，那么我们就直接将最后一个节点的cnt减一，第三种就是你要删除的字符串也有其余的字符串有相同的前缀，比如abbe与abde就有相同的，所以我们就要判断节点下面是否还有其余的非NULL节点，如果有就不删除，没有就删除节点，

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
bool Delete(node* root,char s[],int pos,int ls)
{
	bool flag;//判断该节点是否还有next指向的非NULL节点 
	if(pos!=ls)
	{
		flag=Delete(root->next[s[pos]-'a'],s,pos+1,ls);
		if(!flag)
		{
			root->next[s[pos] - 'a'] = NULL;
			if (root->cnt)
			{
				delete root;
				return false;
			}
		}
		return true;
	}
	else
	{
		root->cnt--;
		for(int i=0;i<26;i++)
		{
			if(root->next[i]!=NULL)
			return true;
		}
		if(root->cnt)
		return true;
		else
		{
			delete root;
			return false; 
		}
	}
}

上面的代码是空间动态建树的代码，数组模拟建树代码

小结

Trie树的基本性质可以归纳为：
（1）根节点不包含字符，除根节点意外每个节点只包含一个字符。
（2）从根节点到某一个节点，路径上经过的字符连接起来，为该节点对应的字符串。
（3）每个节点的所有子节点包含的字符串不相同。
Trie树有一些特性：
1）根节点不包含字符，除根节点外每一个节点都只包含一个字符。
2）从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
3）每个节点的所有子节点包含的字符都不相同。
4）如果字符的种数为n，则每个结点的出度为n，这也是空间换时间的体现，浪费了很多的空间。
5）插入查找的复杂度为O(n)，n为字符串长度。
出自博客