小北
0%

线段树

发表于 分类于

今天要写的是线段树，刚学，趁热打铁赶紧写下来，不然又忘了！

线段树简述

对于一个区间长度长的数据，我们要对其查询某一段的和和修改某一个值，有两种常用方法:
1.用一个数组记录值，修改的话直接对着数组修改，时间复杂度为o(1),但在我们后续查询的过程中，要对其求和，就得一个个去加起来，这样的复杂度为o(n);
2.使用前缀和，用sum[n]数组去求前n个数组的和，在求区间[L,R]的时候也只需要用sum[R]-sum[L],这样的方法使得求和的速度比第一种方法快，但在修改的时候，我们要修改一个数值，我们就得更新sum[]数组的值，使得整个区间的sum都得去改变，这样更新的复杂度又是高的

前面两种方法在一定程度上虽然能使得我们对一个区间能进行更新与求和，但遇到长度长的数据在这两种方法中选择也是有不同的缺点的，这样我们就可以使用线段树来代替前面两种方法。

线段树是以二叉树为基础的，用二分的思想进行处理。

线段树的建立

eg: 对一个区间[0,5]
我们可以将树建立成如下：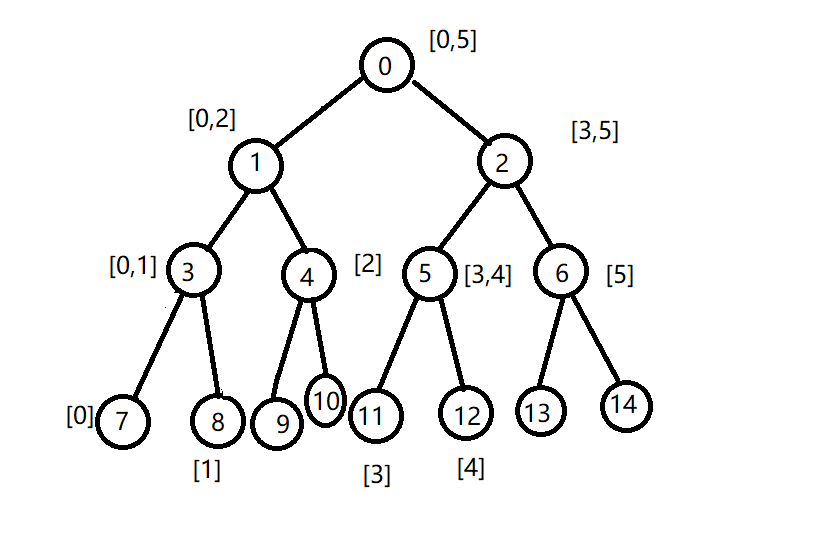
alt

以0为根节点，我们可以看到一个节点有左右两个子节点，设根节点为node，node_lefe=2node+1,node_right=2node+2;第一个根节点所代表的区间为整个区间，在我这里所表示的是[0,5],下面用二分的方法来建立子节点所代表的区间

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void build_tree(int a[],int tree[],int node,int start,int end)//a[]为原数组的值，tree[]是我们建立树的结点的值，node为根节点
{
	if(start==end)  //直到start==end不再递归，将a[start]或a[end]的任意一值赋值给tree[node]
	tree[node]=a[start];
	else
	{
		int node_left=2*node+1;//左节点
		int node_right=2*node+2;//右节点
		int mid=(start+end)/2;
		build_tree(a,tree,node_left,start,mid);
		build_tree(a,tree,node_right,mid+1,end);
		tree[node]=tree[node_left]+tree[node_right];
	}
}

线段树的更新

在建立线段树的基础上，我们在函数中再加入id，num两个值，即可确立更新函数，id是a数组的下标，num是要改动的值，即a[id]=num;在树的更新中，我们首先也是要找到中间值，确定区间，如果 id>=start&&id<=mid 那我们就要去左边区间寻找节点并进行更新，递归，知道start==end,那就将a[id]的值改成num,然后再把tree[node]的值也进行更改为num，然后就可以将线段树进行更新了。
代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
void updata(int a[],int tree[],int node,int start,int end,int id,int num)//id是a数组的下标，num是要改动的值，即a[id]=num; 
{
	if(start==end)
	{
		a[id]=num;
		tree[node]=num;
	}
	else
	{
		int mid=(start+end)/2;//确定中间点
		int node_left=2*node+1;
		int node_right=2*node+2;
		if(id>=start&&id<=mid)
		{
			updata(a,tree,node_left,start,mid,id,num);
		}
		else
		{
			updata(a,tree,node_right,mid+1,end,id,num);
		} 
		tree[node]=tree[node_left]+tree[node_right];
	}
}

线段树的查询

我们要查询区间[L,R]的和，那我们也得像前面一样，从根节点开始去寻找区间所在的位置，但在这里我们可以简化的是，当我们要查询的[start,end]在我们的[L,R]区间的时候，我们就可以直接返回这个节点的tree[node]的值，不需要他继续往后面去查询返回，也需要注意，当我们所要找的区间不在我们即将查询的范围时，我们就就需要退出，而查询也像前面一样，用二分的方法去查询，最后函数以sum_left+sum_right的值返回。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int query_tree(int a[],int tree[],int node,int start,int end,int L,int R)//L,R是查询区间
{
	if(start>R||L>end)
	{
		return 0;
	}
	else if(L<=start&&end<=R)
	{
		return tree[node];
	}
	else 
	{
		int mid=(start+end)/2;
		int node_left=2*node+1;
		int node_right=2*node+2;
		int sum_left=query_tree(a,tree,node_left,start,mid,L,R);
		int sum_right=query_tree(a,tree,node_right,mid+1,end,L,R);
		return sum_left+sum_right;
	}
}

线段树例题(hhh,待更新)

线段树的局部代码全部在这里了，全部代码待我更新例题，我突然发现，我学的这种方法，跟学长讲的有丢不一样，看来我得过会儿去康康学长的方法了。